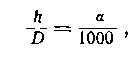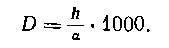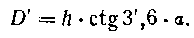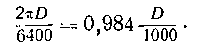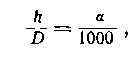
Пусть в прямоугольном треугольнике высота !г составляет а тысячных дистанции D (большой катет), т. е. имеем равенство

отсюда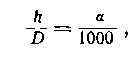

С другой стороны,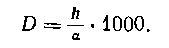

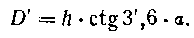
Отношение -^£)~^£)- дает относительную ошибку, которую мы делаем при

определении дистанции по упрощенной первой формуле. Табл. 5 дает сопоставление измеряемых дистанций и величины относительных ошибок при разных углах а (Л принято равным 100 м).

Таблица 5

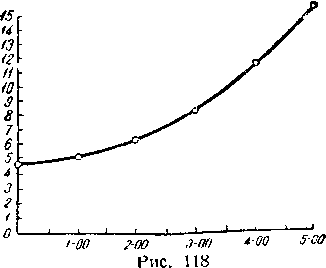
График на рис. 118 иллюстрирует эту таблицу. По горизонтальной оси отложены углы а в тысячных, по вертикальной оси — относительные ошибки в процентах. Из графика видно, что до углов а = 3-00 ошибки возрастают медленно, оставаясь в пределах 5—8%, но после угла 3-00 очень быстро растут. Таблица

показывает, что мы измеряем все дистанции с возрастающей ошибкой и получаем все время результаты, которые больше, чем истинная дистанция D'. Поэтому такой очень простой и быстрый способ измерения дистанции можно рекомендовать только для углов а, меньших 3-00.

Во французской армии принята другая мера углов, там вся окружность делится на 6400 частей; такая «тысячная» составляет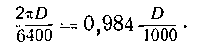

Эта тысячная отклоняется в другую сторону и при малых углах отличается на 1,6% от длины дуги, равной

Измерение при помощи такой тысячной будет давать меньшие дистанции, чем действительные, однако, ошибки здесь будут, примерно, в три раза меньше, чем при пользовании «русской тысячной». Изменение относительных ошибок в зависимости от измеряемого угла будет такое же, только ординаты графика рис. 118 необходимо уменьшить втрое.

После войны 1914— 1918 гг. во Франции было решено ввести в армии единую

систему измерения углов: в градах (щ окружности), с подразделениями на десятые доли града. 1 град равен 54' или 0-15 тысячным по принятой у нас системе делений. В различных армиях и странах существовали (и отчасти продолжают